- #Z score standard normal table how to#
- #Z score standard normal table code#
Using some simple subtraction, you can also find the area to the right of a z-score, or the area between z-scores with the z-table. The z-table is a chart of numbers that we use to identify the area under the normal curve to the left of a z-score.
#Z score standard normal table how to#
In this article, I’ll walk you through how to use the z-table, or z-score table.
How To Use the Z-Table to Find Area and Z-Scores. How to Find a Z-Score with the Z-Score Formula. What is a Z-Score? Why We Use Them and What They Mean. Outlier Calculator with Easy Step-by-Step Solution. Standard Deviation Calculator with Step by Step Solution. 5 Number Summary Calculator / IQR Calculator. Range, Standard Deviation, and Variance Calculator. #Z score standard normal table code#
The comparison doesn’t require any hard code formula. So, by this z score table, we can easily compare the values of different aspects.
It is a crystal clear table as in its reliability and credibility. The tests that are taken from the data at interval management are traced by this table. It plays a significant role in comparing the raw figures of the data. So, 1.45 standard deviation is the shaded one in the standard normal curve. In order to find the area of 0.4265, we have to read across the table of 0.5. Let’s assume that the area within is 1.45 standard deviation above the mean. The normal curve shows the mean as 0 and the standard deviation is 1. Now, you can trace the value in the z table and that will take you to the percentage score of -1.34. The area below the z curve starts from the left side of the graph. State the percentage of score that lies below 73. The distribution of test scores has a mean of 80 and a standard deviation of 5.2. 
Let’s understand this concept with an example: Example1 It is equal to the area of the distribution above Z.
The complementary cumulative, which provides a figure more than Z. 
The cumulative, that provides a statistical value less than Z or the area of below the distribution. The cumulative, from the mean that it provides a statistic value between 0 and Z. It means the shaded portion below the curve is the answer and it gives you a better idea of the figures. The area below the z curve is the one, that needs to be calculated. Don’t get confused with the right and left side of the mean. Here μ is the population mean, σ is the population standard deviation, and x is the sample size.Īfter this calculation, you need to look up in the table. The formula to convert a sample mean, X, to a z-score is: The left defines the negative values and the right shows the positive values. So, this approach makes better understanding as well as the solution to the problem. Now, the question arises about why there are two separate z tables? Because we have two values which are positive and negative. It is positive when it lies above the mean. Remember, the z- score shows the number of standard deviations where the value lies below the mean. 
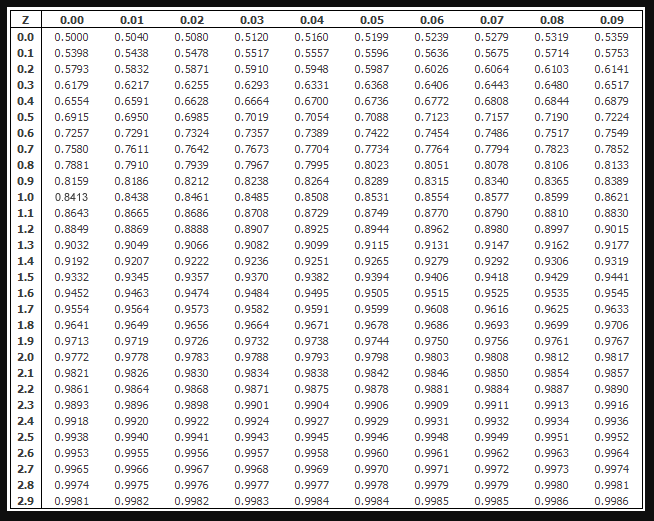
Whether it is above, below, or between the values of normal distribution. It is using to find the probability of statistic value. He was a Belgian astronomer and he linked this distribution and the z curve. This phenomenon was first considered by Lambert Quetelet.
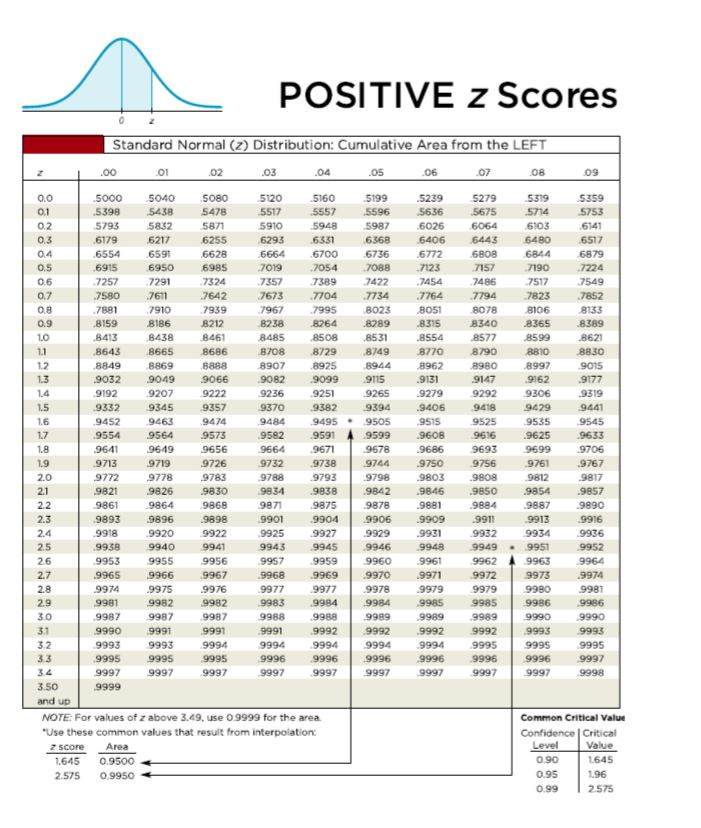
It reflects the area of the z curve on the graph for standard deviations.įor instance, standard distribution is using to show the variables of height, weight, and strength. Z table is simply a standard normal distribution of percentage from 1 to 100. So, he devised a bell-shaped figure on the graph that we usually call the z curve. A French mathematician Abraham de Moivre was interested in gambling and used to find probabilities of the coin flips. Z table, an alphabetical term in the world of mathematics has its interesting origins from history.
0 kommentar(er)
